INTERACTION OF AN EIGENSTATE WITH THE
ONE-PARAMETER EIGENVALUE BAND
Tomislav P. zivkovic
Rudjer Boskovic Institute,
POB 180, HR-1000 Zagreb, Croatia
Interaction of a quantum system 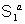 containing a single
state containing a single
state 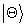 with a known
infinite dimensional quantum system with a known
infinite dimensional quantum system 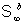 containing an
eigenvalue band containing an
eigenvalue band 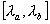 is considered. A
new approach for the treatment of the combined system is considered. A
new approach for the treatment of the combined system 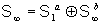 is developed. This
system contains embedded eigenstates is developed. This
system contains embedded eigenstates 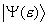 with continuous
eigenvalues with continuous
eigenvalues 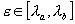 , and in addition it may contain isolated eigenstates , and in addition it may contain isolated eigenstates 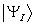 with discrete
eigenvalues with discrete
eigenvalues 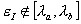 . Exact expressions for the solution of the combined system
are derived. In particular, due to the interaction with the system . Exact expressions for the solution of the combined system
are derived. In particular, due to the interaction with the system 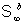 , eigenvalue , eigenvalue 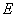 of the state of the state 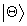 shifts and in
addition if shifts and in
addition if 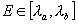 this shifted
eigenvalue broadens. Exact expressions for the eigenvalue shift and for the
eigenvalue distribution of the state this shifted
eigenvalue broadens. Exact expressions for the eigenvalue shift and for the
eigenvalue distribution of the state 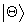 are derived. In the
case of the weak coupling this eigenvalue distribution reduces to the
standard resonance curve. Also, exact expressions for the time evolution of
the state are derived. In the
case of the weak coupling this eigenvalue distribution reduces to the
standard resonance curve. Also, exact expressions for the time evolution of
the state 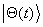 that is initially
prepared in the state that is initially
prepared in the state 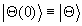 are obtained. Here
again in the case of the weak coupling this time evolution reduces to the
familiar exponential decay. The suggested method is exact and it applies to
each coupling of the system are obtained. Here
again in the case of the weak coupling this time evolution reduces to the
familiar exponential decay. The suggested method is exact and it applies to
each coupling of the system 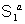 with the system with the system 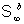 , however strong. It also presents a relatively good
approximation for the interaction of a nondegenerate eigenstate , however strong. It also presents a relatively good
approximation for the interaction of a nondegenerate eigenstate 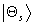 of an arbitrary
system of an arbitrary
system 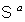 with an infinite
system with an infinite
system 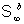 containing a single
eigenvalue band, provided this eigenstate is relatively well separated from
other eigenstates of containing a single
eigenvalue band, provided this eigenstate is relatively well separated from
other eigenstates of 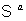 and provided the
interaction between the systems and provided the
interaction between the systems 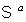 and and 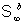 is not excessively
strong. is not excessively
strong.
|