Self-optimising
molecular descriptors
Giorgi Lekishvili and Johann Gasteiger
Computer-Chemie-Centrum,
University of Erlangen-Nuremberg, D-91052 Erlangen, Germany
In the past
few years some descriptors were designed that contained not only considering
the molecular structure, but also had free parameters, or variables. The
numerical values of such free parameters are by no means dependent on the
molecular structure but have to be optimised to achieve maximal performance
of the model. The success of employing this approach crucially depends on the
two following points: a refined strategy of how to vary the free parameters,
as this must not be done by hand, and a substantial mathematical proof that
the models obtained are not simply the by-chance ones fit for the particular
dataset.
This work presents a
generalized form of the self-optimising indices. Our approach is based on a
modern part of mathematics, the lambda calculus.
Let B be the basis of a structural
representation of a molecule, such as the adjacency matrix/connectivity
table, or a vector containing the number of occurrences of different
substructures in the molecule, etc. Let T be an expression possibly
containing B. Then, a self-optimising index is a lambda function
F of B: lB.T(B). Here l is the so-called abstractor. For the particular case, i.e., given
a numerical value of B for the molecule M, bM, the
expression is reduced to a numerical value, DescrM,
as shown below:
(lB.T(B))bM->F(M)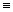 DescrM DescrM
In a simplified case, one has to have a basic form
for the T expression, which will be further optimised for particular tasks.
In our studies, we have applied the autocorrelation polynomial as the
expression and simulated annealing as a technique to optimise it.
Alternatively, neural networks could be applied. Thereafter, one can decrease
the number of candidate descriptors from several hundreds to less than ten
polynomials.
In the most profound case, the genetic programming
can be applied to find the optimal expression of the self-optimising
descriptor.
|