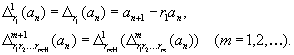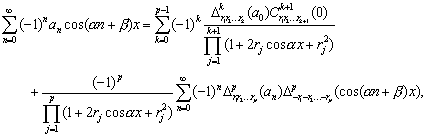Abstract: MATH/CHEM/COMP 2002, Dubrovnik, June 24-29, 2002

Applying an Euler type transformation for accelerating convergence of trigonometric series

Faton M. Berisha and Muharrem Q. Berisha

Faculty of Mathematical and Natural Sciences, University of Prishtina, Prishtina,Kosova

For a sequence of real or complex numbers  and a given sequence  the linear operator  is defined by

Theorem 1. Let  be a convergent real or complex trigonometric series and  a sequence of real or complex numbers such that . Then the following equation holds true

  (1)

where are .

Corollary 1. If there exist the finite limits  , then series on the left-hand side of (1) converges faster then the series

on the right-hand side.

The acceleration of convergence is increased with the value of p.

Example 1. Let . Then  Obviously, for every integer p the sequence  satisfies the conditions of Corollary 1. In particular, in order to calculate the approximate sum of the series  with an error not greater than  we must compute the sum of first 9 terms. Applying the transformation (1), the same accuracy is obtained by computing the sum of 5 terms for , 3 terms for  and 1 term for .